Bicycle and motorcycle dynamics

A computer-generated, simplified model of bike and rider demonstrating an uncontrolled right turn.

Bicycle and motorcycle dynamics is the science of the motion of bicycles and motorcycles and their components, due to the forces acting on them. Dynamics is a branch of classical mechanics, which in turn is a branch of physics. Bike motions of interest include balancing,
steering, braking, accelerating, suspension activation, and vibration. The study of these motions began in the late 19th century and continues today.

Bicycles and motorcycles are both single-track vehicles and so their motions have many fundamental attributes in common and are fundamentally different from and more difficult to study than other wheeled vehicles such as dicycles, tricycles, and quadracycles. As with unicycles, bikes lack lateral stability when stationary, and under most circumstances can only remain upright when moving forward. Experimentation and mathematical analysis have shown that a bike stays upright when it is steered to keep its center of mass over its wheels. This steering is usually supplied by a rider, or in certain circumstances, by the bike itself. Several factors, including geometry, mass distribution, and gyroscopic effect all contribute to varying degrees to this self-stability, but long-standing hypotheses and claims that gyroscopic effect is the main stabilizing force have been discredited.

Animation of a computer-generated, simplified model of bike and passive rider demonstrating uncontrolled weave.

While remaining upright may be the primary goal of beginning riders, a bike must lean in order to maintain balance in a turn: the higher the speed or smaller the turn radius, the more lean is required. This balances the roll torque about the wheel contact patches generated by centrifugal force due to the turn with that of the gravitational force. This lean is usually produced by a momentary steering in the opposite direction, a maneuver often referred to as countersteering. Unlike other wheeled vehicles, the primary control input on bikes is steering torque, not position.

Although longitudinally stable when stationary, bikes often have a high enough center of mass and a short enough wheelbase to lift a wheel off the ground under sufficient acceleration or deceleration. When braking, depending on the location of the combined center of mass of the bike and rider with respect to the point where the front wheel contacts the ground, bikes can either skid the front wheel or flip the bike and rider over the front wheel. A similar situation is possible while accelerating, but with respect to the rear wheel.

History

The history of the study of bike dynamics is nearly as old as the bicycle itself. It includes contributions from famous scientists such as Rankine, Appell, and Whipple. In the early 19th century Karl von Drais, credited with inventing the two-wheeled vehicle variously called the laufmaschine, velocipede, draisine, and dandy horse, showed that a rider could balance his device by steering the front wheel. By the end of the 19th century, Emmanuel Carvallo and Francis Whipple showed with rigid-body dynamics that some safety bicycles could actually balance themselves if moving at the right speed. It is not clear to whom should go the credit for tilting the steering axis from the vertical which helps make this possible.

Bicycles leaning in a turn.

In 1970, David Jones published an article in Physics Today showing that gyroscopic effects are not necessary to balance a bicycle. Since 1971, when he named the weave and capsize modes, Robin Sharp has written about the mathematical behavior of motorcycles and bicycles, and his work has continued to the present day with David Limebeer. Both men were at Imperial College, London. In 2007, Meijaard, Papadopoulos, Ruina, and Schwab published the canonical linearized equations of motion, in the Proceedings of the Royal Society A, along with verification by two different methods.

Draisine.

Forces

If the bike and rider are considered to be a single system, the forces that act on that system and its components can be roughly divided into two groups: internal and external. The external forces are due to gravity, inertia, contact with the ground, and contact with the atmosphere. The internal forces are caused by the rider and by interaction between components.

External forces

External forces on a bike and rider leaning in a turn: gravity in green, drag in blue,
vertical ground reaction in red, net propulsive and rolling resistance in yellow,
friction in response to turn in orange, and net torques on front wheel in magenta.

As with all masses, gravity pulls the rider and all the bike components toward the earth. At each tire contact patch there are ground reaction forces with both horizontal and vertical components. The vertical components mostly counteract the force of gravity, but also vary with braking and accelerating. For details, see the section on longitudinal stability below. The horizontal components, due to friction between the wheels and the ground, including rolling resistance, are in response to propulsive forces, braking forces, and turning forces. Aerodynamic forces due to the atmosphere are mostly in the form of drag, but can also be from crosswinds. At normal bicycling speeds on level ground, aerodynamic drag is the largest force resisting forward motion. At faster speed, aerodynamic drag becomes overwhelmingly the largest force resisting forward motion.

Turning forces are generated during maneuvers for balancing in addition to just changing direction of travel. These may be interpreted as centrifugal forces in the accelerating reference frame of the bike and rider; or simply as inertia in a stationary, inertial reference frame and not forces at all. Gyroscopic forces acting on rotating parts such as wheels, engine, transmission, etc., are also due to the inertia of those rotating parts. They are discussed further in the section on gyroscopic effects below.

Internal forces

Internal forces are mostly caused by the rider or by friction. The rider can apply torques between the steering mechanism (front fork, handlebars, front wheel, etc.) and rear frame, and between the rider and the rear frame. Friction exists between any parts that move against each other: in the drive train, between the steering mechanism and the rear frame, etc. Many bikes have front and rear suspensions, and some motorcycles have a steering damper to dissipate undesirable kinetic energy. On bikes with rear suspensions, feedback between the drive train and the suspension is an issue designers attempt to handle with various linkage configurations and dampers.

Motions

Motions of a bike can be roughly grouped into those out of the central plane of symmetry: lateral; and those in the central plane of symmetry: longitudinal or vertical. Lateral motions include balancing, leaning, steering, and turning. Motions in the central plane of symmetry include rolling forward, of course, but also stoppies, wheelies, brake diving, and most suspension activation. Motions in these two groups are linearly decoupled, that is they do not interact with each other to the first order. An uncontrolled bike is laterally unstable when stationary and can be laterally self-stable when moving under the right conditions or when controlled by a rider. Conversely, a bike is longitudinally stable when stationary and can be longitudinally unstable when undergoing sufficient acceleration or deceleration.

Lateral dynamics

Of the two, lateral dynamics has proven to be the more complicated, requiring three-dimensional, multibody dynamic analysis with at least two generalized coordinates to analyze. At a minimum, two coupled, second-order differential equations are required to capture the principal motions. Exact solutions are not possible, and numerical methods must be used instead. Competing theories of how bikes balance can still be found in print and online. On the other hand, as shown in later sections, much longitudinal dynamic analysis can be accomplished simply with planar kinetics and just one coordinate.

Balance

A bike remains upright when it is steered so that the ground reaction forces exactly balance all the other internal and external forces it experiences, such as gravitational if leaning, inertial or centrifugal if in a turn, gyroscopic if being steered, and aerodynamic if in a crosswind. Steering may be supplied by a rider or, under certain circumstances, by the bike itself. This self-stability is generated by a combination of several effects that depend on the geometry, mass distribution, and forward speed of the bike. Tires, suspension, steering damping, and frame flex can also influence it, especially in motorcycles.

Balancing a bicycle by keeping the wheels under the center of mass

Even when staying relatively motionless, a rider can balance a bike by the same principle. While performing a track stand, the rider can keep the line between the two contact patches under the combined center of mass by steering the front wheel to one side or the other and then moving forward and backward slightly to move the front contact patch from side to side as necessary. Forward motion can be generated simply by pedaling. Backwards motion can be generated the same way on a fixed-gear bicycle. Otherwise, the rider can take advantage of an opportune slope of the pavement or lurch the upper body backwards while the brakes are momentarily engaged.

If the steering of a bike is locked, it becomes virtually impossible to balance while riding. On the other hand, if the gyroscopic effect of rotating bike wheels is cancelled by adding counter-rotating wheels, it is still easy to balance while riding.

Forward speed

The rider applies torque to the handlebars in order to turn the front wheel and so to control lean and maintain balance. At high speeds, small steering angles quickly move the ground contact points laterally; at low speeds, larger steering angles are required to achieve the same results in the same amount of time. Because of this, it is usually easier to maintain balance at high speeds.

Center of mass location

The farther forward (closer to front wheel) the center of mass of the combined bike and rider, the less the front wheel has to move laterally in order to maintain balance. Conversely, the further back (closer to the rear wheel) the center of mass is located, the more front wheel lateral movement or bike forward motion will be required to regain balance. This can be noticeable on long-wheelbase recumbents and choppers. It can also be an issue for touring bikes with a heavy load of gear over or even behind the rear wheel. Mass over the rear wheel can be more easily controlled if it is lower than mass over the front wheel.

A bike is also an example of an inverted pendulum. Just as a broomstick is easier to balance than a pencil, a tall bike (with a high center of mass) can be easier to balance when ridden than a low one because its lean rate will be slower. However, a rider can have the opposite impression of a bike when it is stationary. A top-heavy bike can require more effort to keep upright, when stopped in traffic for example, than a bike which is just as tall but with a lower center of mass. This is an example of a vertical second-class lever. A small force at the end of the lever, the seat or handlebars at the top of the bike, more easily moves a large mass if the mass is closer to the fulcrum, where the tires touch the ground. This is why touring cyclists are advised to carry loads low on a bike, and panniers hang down on either side of front and rear racks.

Trail

A factor that influences how easy or difficult a bike will be to ride is trail, the distance that the front wheel ground contact point trails behind the steering axis ground contact point. The steering axis is the axis about which the entire steering mechanism (fork, handlebars, front wheel, etc.) pivots. In traditional bike designs, with a steering axis tilted back from the vertical, trail causes the front wheel to steer into the direction of a lean, independent of forward speed. This can be seen by pushing a stationary bike to one side. The front wheel will usually also steer to that side. In a lean, gravity provides this force.

Bicycle head angle, rake, and trail

Trail is a function of head angle, fork offset or rake, and wheel size. Their relationship can be described by this formula:

where Rw is wheel radius, Ah is the head angle measured clock-wise from the horizontal and Of is the fork offset or rake. Trail can be increased by increasing the wheel size, decreasing or slackening the head angle, or decreasing the fork rake.

The more trail a bike has, the more stable it feels. Bikes with negative trail (where the contact patch is actually in front of where the steering axis intersects the ground), while still ridable, feel very unstable. Bikes with too much trail feel difficult to steer. Normally, road racing bicycles have more trail than mountain bikes or touring bikes. In the case of mountain bikes, less trail allows more accurate path selection off-road, and also allows the rider to recover from obstacles on the trail which might knock the front wheel off course. Touring bikes are built with small trail to allow the rider to control a bike weighed down with baggage. As a consequence, an unloaded touring bike can feel unstable. In bicycles, fork rake, often a curve in the fork blades forward of the steering axis, is used to diminish trail. In motorcycles, rake refers to the head angle instead, and offset created by the triple tree is used to diminish trail.

A small survey by Whitt and Wilson found:

• touring bicycles with head angles between 72° and 73° and trail between 43 mm and 60 mm
• racing bicycles with head angles between 73° and 74° and trail between 28 mm and 45 mm
• track bicycles with head angles of 75° and trail between 23.5 mm and 37 mm.

However, these ranges are not hard and fast. For example, LeMond Racing Cycles offers both with forks that have 45 mm of offset or rake and the same size wheels:

• a 2006 Tete de Course, designed for road racing, with a head angle that varies from 71¼° to 74°, depending on frame size, and thus trail that varies from 69 mm to 51.5 mm.
• a 2007 Filmore, designed for the track, with a head angle that varies from 72½° to 74°, depending on frame size, and thus trail that varies from 61 mm to 51.5 mm.

The amount of trail a particular bike has may vary with time for several reasons. On bikes with front suspension, especially telescopic forks, compressing the front suspension, due to heavy braking for example, can steepen the steering axis angle and reduce trail. Trail also varies with lean angle, and steering angle, usually decreasing from a maximum when the bike is straight upright and steered straight ahead. Finally, even the profile of the front tire can influence how trail varies as the bike is leaned and steered.

A measurement similar to trail, called either mechanical trail, normal trail, or true trail, is the perpendicular distance from the steering axis to the centroid of the front wheel contact patch.

Steering mechanism mass distribution

Another factor that can also contribute to the self-stability of traditional bike designs is the distribution of mass in the steering mechanism, which includes the front wheel, the fork, and the handlebar. If the center of mass for the steering mechanism is in front of the steering axis, then the pull of gravity will also cause the front wheel to steer in the direction of a lean. This can be seen by leaning a stationary bike to one side. The front wheel will usually also steer to that side independent of any interaction with the ground. Additional parameters, such as the fore-to-aft position of the center of mass and the elevation of the center of mass also contribute to the dynamic behavior of a bike.

Gyroscopic effects

The role of the gyroscopic effect in most bike designs is to help steer the front wheel into the direction of a lean. This phenomenon is called precession and the rate at which an object precesses is inversely proportional to its rate of spin. The slower a front wheel spins, the faster it will precess when the bike leans, and vice-versa. The rear wheel is prevented from precessing as the front wheel does by friction of the tires on the ground, and so continues to lean as though it were not spinning at all. Hence gyroscopic forces do not provide any resistance to tipping.

Gyroscopic effect on front wheel of a bike. Appling a torque (in green)
about the lean axis results in a reaction torque (in blue) about the steer axis.

At low forward speeds, the precession of the front wheel is too quick, contributing to an uncontrolled bike’s tendency to oversteer, start to lean the other way and eventually oscillate and fall over. At high forward speeds, the precession is usually too slow, contributing to an uncontrolled bike’s tendency to understeer and eventually fall over without ever having reached the upright position. This instability is very slow, on the order of seconds, and is easy for most riders to counteract. Thus a fast bike may feel stable even though it is actually not self-stable and would fall over if it were uncontrolled. A bicycle wheel with an internal flywheel for enhanced gyroscopic effect is under development as a commercial product, the Gyrobike, for making it easier to learn to ride bicycles.

Another contribution of gyroscopic effects is a roll moment generated by the front wheel during countersteering. For example, steering left causes a moment to the right. The moment is small compared to the moment generated by the out-tracking front wheel, but begins as soon as the rider applies torque to the handlebars and so can be helpful in motorcycle racing. For more detail, see the countersteering article.

Self-stability

Between the two unstable regimes mentioned in the previous section, and influenced by all the factors described above that contribute to balance (trail, mass distribution, gyroscopic effects, etc.), there may be a range of forward speeds for a given bike design at which these effects steer an uncontrolled bike upright.

However, even without self-stability a bike may be ridden by steering it to keep it over its wheels. Note that the effects mentioned above that would combine to produce self-stability may be overwhelmed by additional factors such as headset friction and stiff control cables. This video shows a riderless bicycle exhibiting self-stability.

Turning

Motorcycles leaning in a turn.

In order to turn a bike, that is, change its direction of forward travel, the front wheel is turned approximately in the desired direction, as with any front-wheel steered vehicle. Friction between the wheels and the ground then generates the centripetal acceleration necessary to alter the course from straight ahead as a combination of cornering force and camber thrust. The radius of the turn of an upright (not leaning) bike can be roughly approximated, for small steering angles, by:

where r is the approximate radius, w is the wheelbase, δ is the steer angle, and φ is the caster angle of the steering axis.

Leaning

However, unlike other wheeled vehicles, bikes must also lean during a turn to balance the relevant forces: gravitational, inertial, frictional, and ground support. The angle of lean, θ, can easily be calculated using the laws of circular motion:

where v is the forward speed, r is the radius of the turn and g is the acceleration of gravity. This is in the idealized case. A slight increase in the lean angle may be required on motorcycles to compensate for the width of modern tires at the same forward speed and turn radius.

The forces acting on a leaning bike in the rotating reference frame of a turn
where N is the normal force,F_f is friction, m is mass, r is turn radius, v is forward speed, and g is the acceleration of gravity.

For example, a bike in a 10 m (33 ft) radius steady-state turn at 10 m/s (22 mph) must be at an angle of 45°. A rider can lean with respect to the bike in order to keep either the torso or the bike more or less upright if desired. The angle that matters is the one between the horizontal plane and the plane defined by the tire contacts and the location of the center of mass of bike and rider.

This lean of the bike decreases the actual radius of the turn proportionally to the cosine of the lean angle. The resulting radius can be roughly approximated (within 2% of exact value) by:

where r is the approximate radius, w is the wheelbase, θ is the lean angle, δ is the steer angle, and φ is the caster angle of the steering axis. As a bike leans, the tires' contact patches move farther to the side causing wear. The portions at either edge of a motorcycle tire that remain unworn by leaning into turns is sometimes referred to as chicken strips.

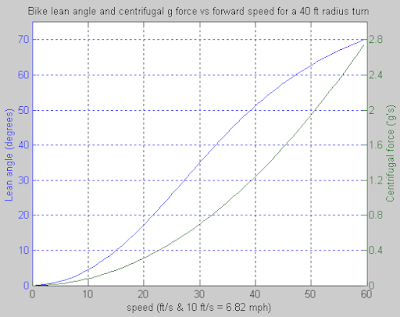Graph of bike lean angle vs forward speed, assuming unlimited friction between tires and ground.

Countersteering

In order to initiate a turn and the necessary lean in the direction of that turn, a bike must momentarily steer in the opposite direction. This is often referred to as countersteering. With the front wheel now at an angle to the direction of motion, a lateral force is developed at the contact patch of the tire. This force creates a torque around the longitudinal (roll) axis of the bike. This torque causes the bike to roll in the opposite direction of the turn. Where there is no external influence, such as an opportune side wind to create the force necessary to lean the bike, countersteering happens in every turn.

Cyclist riding with no hands on the handlebars.

As the lean approaches the desired angle, the front wheel must be steered in the direction of the turn, depending on the forward speed, the turn radius, and the need to maintain the lean angle. Once in a turn, the radius can only be changed with an appropriate change in lean angle. This can only be accomplished by additional countersteering out of the turn to increase lean and decrease radius, then into the turn to decrease lean and increase radius. To exit the turn, the bike must again countersteer, momentarily steering more into the turn in order to decrease the radius, thus increasing inertial forces, and thereby decreasing the angle of lean.

Steady-state turning

Once a turn is established, the torque that must be applied to the steering mechanism in order to maintain a constant radius at a constant forward speed depends on the forward speed and the geometry and mass distribution of the bike. At speeds below the capsize speed, described below in the section on Eigenvalues and also called the inversion speed, the self-stability of the bike will cause it to tend to steer into the turn, righting itself and exiting the turn, unless a torque is applied in the opposite direction of the turn. At speeds above the capsize speed, the capsize instability will cause it to tend to steer out of the turn, increasing the lean, unless a torque is applied in the direction of the turn. At the capsize speed no input steering torque is necessary to maintain the steady-state turn.

Steering angle

Several effects influence the steering angle, the angle at which the front assembly is rotated about the steering axis, necessary to maintain a steady-state turn. Some of these are unique to single-track vehicles, while others are also experienced by automobiles. Some of these may be mentioned elsewhere in this article, and they are repeated here, though not necessarily in order of importance, so that they may be found in one place.

First, the actual kinematic steering angle, the angle projected onto the road plane to which the front assembly is rotated is a function of the steering angle and the steering axis angle:

where Δ is the kinematic steering angle, δ is the steering angle, and φ is the caster angle of the steering axis.

Second, the lean of the bike decreases the actual radius of the turn proportionally to the cosine of the lean angle. The resulting radius can be roughly approximated (within 2% of exact value) by:

where r is the approximate radius, w is the wheelbase, θ is the lean angle, δ is the steering angle, and φ is the caster angle of the steering axis.

Third, because the front and rear tires can have different slip angles due to weight distribution, tire properties, etc., bikes can experience understeer or oversteer. When understeering, the steering angle must be greater, and when oversteering, the steering angle must be less than it would be if the slip angles were equal to maintain a given turn radius. Some authors even use the term counter-steering to refer to the need on some bikes under some conditions to steer in the opposite direction of the turn (negative steering angle) to maintain control in response to significant rear wheel slippage.

Fourth, camber thrust contributes to the centripetal force necessary to cause the bike to deviate from a straight path, along with cornering force due to the slip angle, and can be the largest contributor. Camber thrust contributes to the ability of bikes to negotiate a turn with the same radius as automobiles but with a smaller steering angle. When a bike is steered and leaned in the same direction, the camber angle of the front tire is greater than that of the rear and so can generate more camber thrust, all else being equal.

No hands

While countersteering is usually initiated by applying torque directly to the handlebars, on lighter vehicles such as bicycles, it can also be accomplished by shifting the rider’s weight. If the rider leans to the right relative to the bike, the bike will lean to the left to conserve angular momentum, and the combined center of mass will remain in the same vertical plane. This leftward lean of the bike, called counter lean by some authors, will cause it to steer to the left and initiate a right-hand turn as if the rider had countersteered to the left by applying a torque directly to the handlebars. Note that this technique may be complicated by additional factors such as headset friction and stiff control cables.

Gyroscopic effects

As mentioned above in the section on balance, one effect of turning the front wheel is a roll moment caused by gyroscopic precession. The magnitude of this moment is proportional to the moment of inertia of the front wheel, its spin rate (forward motion), the rate that the rider turns the front wheel by applying a torque to the handlebars, and the cosine of the angle between the steering axis and the vertical.

For a sample motorcycle moving at 22 m/s (50 mph) that has a front wheel with a moment of inertia of 0.6 kg·m2, turning the front wheel one degree in half a second generates a roll moment of 3.5 N·m. In comparison, the lateral force on the front tire as it tracks out from under the motorcycle reaches a maximum of 50 N. This, acting on the 0.6 m (2 ft) height of the center of mass, generates a roll moment of 30 N·m.

While the moment from gyroscopic forces is only 12% of this, it can play a significant part because it begins to act as soon as the rider applies the torque, instead of building up more slowly as the wheel out-tracks. This can be especially helpful in motorcycle racing.

Two-wheel steering

Because of theoretical benefits, such as a tighter turning radius at low speed, attempts have been made to construct motorcycles with two-wheel steering. One working prototype by Ian Drysdale in Australia is reported to "work very well." Issues in the design include whether to provide active control of the rear wheel or let it swing freely. In the case of active control, the control algorithm needs to decide between steering with or in the opposite direction of the front wheel, when, and how much. One implementation of two-wheel steering, the Sideways bike, lets the rider control the steering of both wheels directly.

Milton W. Raymond built a long low two-wheel steering bicycle, called "X-2", with various steering mechanisms to control the two wheels independently. Steering motions included "balance", in which both wheels move together to steer the tire contact under the center of gravity; and "true circle", in which the wheels steer equally in opposite directions and thus steering the bicycle without substantially changing the lateral position of the tire contacts relative to the center of mass. X-2 was also able to go "crabwise" with the wheels parallel but out of line with the frame, for instance with the front wheel near the roadway center line and rear wheel near the curb. "Balance" steering allowed easy balancing despite long wheelbase and low center of mass, but no self-balancing ("no hands") configuration was discovered. True circle, as expected, was essentially impossible to balance, as steering does not correct for misalignment of the tire patch and center of mass. Crabwise cycling at angles tested up to about 45° did not show a tendency to fall over, even under braking. X-2 is mentioned in passing in Whitt and Wilson's Bicycling Science 2nd edition.

Rear-wheel steering

Because of the theoretical benefits, especially a simplified front-wheel drive mechanism, attempts have been made to construct a ridable rear-wheel steering bike. The Bendix Company built a rear-wheel steering bicycle, and the U.S. Department of Transportation commissioned the construction of a rear-wheel steering motorcycle: both proved to be unridable. Rainbow Trainers, Inc. in Alton, IL, offered US$5,000 to the first person "who can successfully ride the rear-steered bicycle, Rear Steered Bicycle I". One documented example of someone successfully riding a rear-wheel steering bicycle is that of L. H. Laiterman at MIT, on a specially designed recumbent bike. The difficulty is that turning left, accomplished by turning the rear wheel to the right, initially moves the center of mass to the right, and vice versa. This complicates the task of compensating for leans induced by the environment. Examination of the eigenvalues shows that the rear-wheel steering configuration is inherently unstable.

Center steering

Between the extremes of bicycles with classical front-wheel steering and those with strictly rear-wheel steering is a class of bikes with a pivot point somewhere between the two referred to as center-steering, similar to articulated steering. An early implementation of the concept was the Phantom bicycle in the early 1870s promoted as a safer alternative to the penny-farthing This design allows for simple front-wheel drive and current implementations appear to be quite stable, even ridable no-hands, as many photographs illustrate.

Flevobike with center steering

These designs, such as the Python Lowracer, usually have very lax head angles (40° to 65°) and positive or even negative trail. The builder of a bike with negative trail states that steering the bike from straight ahead forces the seat (and thus the rider) to rise slightly and this offsets the destabilizing effect of the negative trail.

Tiller effect

Tiller effect is the expression used to describe how handlebars that extend far behind the steering axis (head tube) act like a tiller on a boat, in that one moves the bars to the right in order to turn the front wheel to the left, and vice versa. This situation is commonly found on cruiser bicycles, some recumbents, and even some cruiser motorcycles. It can be troublesome when it limits the ability to steer because of interference or the limits of arm reach.

Tires

Tires have a large influence over bike handling, especially on motorcycles. Tire inflation pressures have also been found to be important variables in the behavior of a motorcycle at high speeds. Because the front and rear tires can have different slip angles due to weight distribution, tire properties, etc., bikes can experience understeer or oversteer. Of the two, understeer, in which the front wheel slides more than the rear wheel, is more dangerous since front wheel steering is critical for maintaining balance. Also, because real tires have a finite contact patch with the road surface that can generate a scrub torque, and when in a turn, can experience some side slipping as they roll, they can generate torques about an axis normal to the plane of the contact patch.

Bike tire contact patch during a right-hand turn

One torque generated by tires is due to asymmetries in the side-slip along the length of the contact patch. The resultant force of this side-slip occurs behind the geometric center of the contact patch, a distance described as the pneumatic trail, and so creates a torque on the tire. Since the direction of the side-slip is towards the outside of the turn, the force on the tire is towards the center of the turn. Therefore, this torque tends to turn the front wheel in the direction of the side-slip, away from the direction of the turn, and therefore tends to increase the radius of the turn.

Another torque is produced by the finite width of the contact patch and the lean of the tire in a turn. The portion of the contact patch towards the outside of the turn is actually moving rearward, with respect to the wheel's hub, faster than the rest of the contact patch, because of its greater radius from the hub. By the same reasoning, the inner portion is moving rearward more slowly. So the outer and inner portions of the contact patch slip on the pavement in opposite directions, generating a torque that tends to turn the front wheel in the direction of the turn, and therefore tends to decrease the turn radius.

The combination of these two opposite torques creates a resulting yaw torque on the front wheel, and its direction is a function of the side-slip angle of the tire, the angle between the actual path of the tire and the direction it is pointing, and the camber angle of the tire (the angle that the tire leans from the vertical). The result of this torque is often the suppression of the inversion speed predicted by rigid wheel models described above in the section on steady-state turning.

High side

A highsider, highside, or high side is a type of bike motion which is caused by a rear wheel gaining traction when it is not facing in the direction of travel, usually after slipping sideways in a curve. This can occur under heavy braking, acceleration, a varying road surface, or suspension activation, especially due to interaction with the drivetrain. It can take the form of a single slip-then-flip or a series of violent oscillations.

Maneuverability and handling

Bike maneuverability and handling is difficult to quantify for several reasons. The geometry of a bike, especially the steering axis angle makes kinematic analysis complicated. Under many conditions, bikes are inherently unstable and must always be under rider control. Finally, the rider's skill has a large influence on the bike's performance in any maneuver. Bike designs tend to consist of a trade-off between maneuverability and stability.

Rider control inputs

The primary control input that the rider can make is to apply a torque directly to the steering mechanism via the handlebars. Because of the bike's own dynamics, due to steering geometry and gyroscopic effects, direct position control over steering angle has been found to be problematic.

Graphs showing the lean and steer angle response of an otherwise uncontrolled bike,
traveling at a forward speed in its stable range (6 m/s), to a steer torque that begins
 as an impulse and then remains constant. Torque to right causes initial steer to right,
lean to left, and eventually a steady-state turn to left.

A secondary control input that the rider can make is to lean the upper torso relative to the bike. As mentioned above, the effectiveness of rider lean varies inversely with the mass of the bike. On heavy bikes, such as motorcycles, rider lean mostly alters the ground clearance requirements in a turn, improves the view of the road, and improves the bike system dynamics in a very low-frequency passive manner.

Differences from automobiles

The need to keep a bike upright to avoid injury to the rider and damage to the vehicle even limits the type of maneuverability testing that is commonly performed. For example, while automobile enthusiast publications often perform and quote skidpad results, motorcycle publications do not. The need to "set up" for a turn, lean the bike to the appropriate angle, means that the rider must see further ahead than is necessary for a typical car at the same speed, and this need increases more than in proportion to the speed.

Rating schemes

Several schemes have been devised to rate the handling of bikes, particularly motorcycles.

• The roll index is the ratio between steering torque and roll or lean angle.
• The acceleration index is the ratio between steering torque and lateral or centripetal acceleration.
• The steering ratio is the ratio between the theoretical turning radius based on ideal tire behavior and the actual turning radius. Values less than one, where the front wheel side slip is greater than the rear wheel side slip, are described as under-steering; equal to one as neutral steering; and greater than one as over-steering. Values less than zero, in which the front wheel must be turned opposite the direction of the curve due to much greater rear wheel side slip than front wheel have been described as counter-steering. Riders tend to prefer neutral or slight over-steering. Car drivers tend to prefer under-steering.
• The Koch index is the ratio between peak steering torque and the product of peak lean rate and forward speed. Large, touring motorcycles tend to have a high Koch index, sport motorcycles tend to have a medium Koch index, and scooters tend to have a low Koch index. It is easier to maneuver light scooters than heavy motorcycles.

Lateral motion theory

Although its equations of motion can be linearized, a bike is a nonlinear system. The variable(s) to be solved for cannot be written as a linear sum of independent components, i.e. its behavior is not expressible as a sum of the behaviors of its descriptors. Generally, nonlinear systems are difficult to solve and are much less understandable than linear systems. In the idealized case, in which friction and any flexing is ignored, a bike is a conservative system. Damping, however, can still be demonstrated: side-to-side oscillations will decrease with time. Energy added with a sideways jolt to a bike running straight and upright (demonstrating self-stability) is converted into increased forward speed, not lost, as the oscillations die out.

A bike is a nonholonomic system because its outcome is path-dependent. In order to know its exact configuration, especially location, it is necessary to know not only the configuration of its parts, but also their histories: how they have moved over time. This complicates mathematical analysis. Finally, in the language of control theory, a bike exhibits non-minimum phase behavior. It turns in the direction opposite of how it is initially steered, as described above in the section on countersteering

Degrees of freedom

The number of degrees of freedom of a bike depends on the particular model being used. The simplest model that captures the key dynamic features, four rigid bodies with knife edge wheels rolling on a flat smooth surface, has 7 degrees of freedom (configuration variables required to completely describe the location and orientation of all 4 bodies):

Graphs of bike steer angle and lean angle vs turn radius.

1. x coordinate of rear wheel contact point
2. y coordinate of rear wheel contact point
3. orientation angle of rear frame (yaw)
4. rotation angle of rear wheel
5. rotation angle of front wheel
6. lean angle of rear frame (roll)
7. steering angle between rear frame and front end

Adding complexity to the model, such as suspension, tire compliance, frame flex, or rider movement, adds degrees of freedom. While the rear frame does pitch with leaning and steering, the pitch angle is completely constrained by the requirement for both wheels to remain on the ground, and so can be calculated geometrically from the other seven variables. If the location of the bike and the rotation of the wheels are ignored, the first five degrees of freedom can also be ignored, and the bike can be described by just two variables: lean angle and steer angle.

Equations of motion

The equations of motion of an idealized bike, consisting of

• a rigid frame,
• a rigid fork,
• two knife-edged, rigid wheels,
• all connected with frictionless bearings and rolling without friction or slip on a smooth horizontal surface and
• operating at or near the upright and straight-ahead, unstable equilibrium

can be represented by a single fourth-order linearized ordinary differential equation or two coupled second-order differential equations, the lean equation

and the steer equation

where

• θr is the lean angle of the rear assembly,
• ψ is the steer angle of the front assembly relative to the rear assembly and
• Mθ and Mψ are the moments (torques) applied at the rear assembly and the steering axis, respectively. For the analysis of an uncontrolled bike, both are taken to be zero.

These can be represented in matrix form as

where

• M is the symmetrical mass matrix which contains terms that include only the mass and geometry of the bike,
• C is the so-called damping matrix, even though an idealized bike has no dissipation, which contains terms that include the forward speed v and is asymmetric,
• K is the so-called stiffness matrix which contains terms that include the gravitational constant g and v2 and is symmetric in g and asymmetric in v2,
• q is a vector of lean angle and steer angle, and
• f is a vector of external forces, the moments mentioned above.

In this idealized and linearized model, there are many geometric parameters (wheelbase, head angle, mass of each body, wheel radius, etc.), but only four significant variables: lean angle, lean rate, steer angle, and steer rate. These equations have been verified by comparison with multiple numeric models derived completely independently

Eigenvalues

It is possible to calculate eigenvalues, one for each of the four state variables (lean angle, lean rate, steer angle, and steer rate), from the linearized equations in order to analyze the normal modes and self-stability of a particular bike design. In the plot to the right, eigenvalues of one particular bicycle are calculated for forward speeds of 0–10 m/s (22 mph). When the real parts of all eigenvalues (shown in dark blue) are negative, the bike is self-stable. When the imaginary parts of any eigenvalues (shown in cyan) are non-zero, the bike exhibits oscillation. The eigenvalues are point symmetric about the origin and so any bike design with a self-stable region in forward speeds will not be self-stable going backwards at the same speed.

Eigenvalues plotted against forward speed for a typical utility bicycle
simplified to have knife-edge wheels that roll without slip.

There are three forward speeds that can be identified in the plot to the right at which the motion of the bike changes qualitatively:

1. The forward speed at which oscillations begin, at about 1 m/s (2.2 mph) in this example, sometimes called the double root speed due to there being a repeated root to the characteristic polynomial (two of the four eigenvalues have exactly the same value). Below this speed, the bike simply falls over as an inverted pendulum does.
2. The forward speed at which oscillations do not increase, where the weave mode eigenvalues switch from positive to negative in a Hopf bifurcation at about 5.3 m/s (12 mph) in this example, is called the weave speed. Below this speed, oscillations increase until the uncontrolled bike falls over. Above this speed, oscillations eventually die out.
3. The forward speed at which non-oscillatory leaning increases, where the capsize mode eigenvalues switch from negative to positive in a pitchfork bifurcation at about 8 m/s (18 mph) in this example, is called the capsize speed. Above this speed, this non-oscillating lean eventually causes the uncontrolled bike to fall over.

Between these last two speeds, if they both exist, is a range of forward speeds at which the particular bike design is self-stable. In the case of the bike whose eigenvalues are shown here, the self-stable range is 5.3–8.0 m/s (12–18 mph). The fourth eigenvalue, which is usually stable (very negative), represents the castoring behavior of the front wheel, as it tends to turn towards the direction in which the bike is traveling. Note that this idealized model does not exhibit the wobble or shimmy and rear wobble instabilities described above. They are seen in models that incorporate tire interaction with the ground or other degrees of freedom.

Experimentation with real bikes has so far confirmed the weave mode predicted by the eigenvalues. It was found that tire slip and frame flex are not important for the lateral dynamics of the bicycle in the speed range up to 6 m/s. The idealized bike model used to calculate the eigenvalues shown here does not incorporate any of the torques that real tires can generate, and so tire interaction with the pavement cannot prevent the capsize mode from becoming unstable at high speeds, as Wilson and Cossalter suggest happens in the real world.

Modes

Graphs that show (from left to right, top to bottom) weave instability, self-stability,
marginal self-stability, and capsize instability in an idealized linearized
model of an uncontrolled utility bicycle.

Bikes, as complex mechanisms, have a variety of modes: fundamental ways that they can move. These modes can be stable or unstable, depending on the bike parameters and its forward speed. In this context, "stable" means that an uncontrolled bike will continue rolling forward without falling over as long as forward speed is maintained. Conversely, "unstable" means that an uncontrolled bike will eventually fall over, even if forward speed is maintained. The modes can be differentiated by the speed at which they switch stability and the relative phases of leaning and steering as the bike experiences that mode. Any bike motion consists of a combination of various amounts of the possible modes, and there are three main modes that a bike can experience: capsize, weave, and wobble. A lesser known mode is rear wobble, and it is usually stable.

Capsize

Capsize is the word used to describe a bike falling over without oscillation. During capsize, an uncontrolled front wheel usually steers in the direction of lean, but never enough to stop the increasing lean, until a very high lean angle is reached, at which point the steering may turn in the opposite direction. A capsize can happen very slowly if the bike is moving forward rapidly. Because the capsize instability is so slow, on the order of seconds, it is easy for the rider to control, and is actually used by the rider to initiate the lean necessary for a turn.

For most bikes, depending on geometry and mass distribution, capsize is stable at low speeds, and becomes less stable as speed increases until it is no longer stable. However, on many bikes, tire interaction with the pavement is sufficient to prevent capsize from becoming unstable at high speeds.

Weave

Weave is the word used to describe a slow (0–4 Hz) oscillation between leaning left and steering right, and vice-versa. The entire bike is affected with significant changes in steering angle, lean angle (roll), and heading angle (yaw). The steering is 180° out of phase with the heading and 90° out of phase with the leaning. This AVI movie shows weave.

For most bikes, depending on geometry and mass distribution, weave is unstable at low speeds, and becomes less pronounced as speed increases until it is no longer unstable. While the amplitude may decrease, the frequency actually increases with speed.

Wobble or shimmy

Eigenvalues plotted against forward speed for a motorcycle modeled with
frame flexibility and realistic tire dynamics. Additional modes can be seen,
such as wobble, which becomes unstable at 43.7 m/s.

The same eigenvalues as in the figure above, but plotted on a root locus plot.
Several additional oscillating modes are visible.

Wobble, shimmy, tank-slapper, speed wobble, and death wobble are all words and phrases used to describe a rapid (4–10 Hz) oscillation of primarily just the front end (front wheel, fork, and handlebars). The rest of the bike remains essentially unaffected. This instability occurs mostly at high speed and is similar to that experienced by shopping cart wheels, airplane landing gear, and automobile front wheels. While wobble or shimmy can be easily remedied by adjusting speed, position, or grip on the handlebar, it can be fatal if left uncontrolled. This AVI movie shows wobble.

Wobble or shimmy begins when some otherwise minor irregularity, such as fork asymmetry, accelerates the wheel to one side. The restoring force is applied in phase with the progress of the irregularity, and the wheel turns to the other side where the process is repeated. If there is insufficient damping in the steering the oscillation will increase until system failure occurs. The oscillation frequency can be changed by changing the forward speed, making the bike stiffer or lighter, or increasing the stiffness of the steering, of which the rider is a main component.

Rear wobble

The term rear wobble is used to describe a mode of oscillation in which lean angle (roll) and heading angle (yaw) are almost in phase and both 180° out of phase with steer angle. The rate of this oscillation is moderate with a maximum of about 6.5 Hz. Rear wobble is heavily damped and falls off quickly as bike speed increases.

Design criteria

The effect that the design parameters of a bike have on these modes can be investigated by examining the eigenvalues of the linearized equations of motion. For more details on the equations of motion and eigenvalues, see the section on the equations of motion above. Some general conclusions that have been drawn are described here.

The lateral and torsional stiffness of the rear frame and the wheel spindle affects wobble-mode damping substantially. Long wheelbase and trail and a flat steering-head angle have been found to increase weave-mode damping. Lateral distortion can be countered by locating the front fork torsional axis as low as possible.

Cornering weave tendencies are amplified by degraded damping of the rear suspension. Cornering, camber stiffnesses and relaxation length of the rear tire make the largest contribution to weave damping. The same parameters of the front tire have a lesser effect. Rear loading also amplifies cornering weave tendencies. Rear load assemblies with appropriate stiffness and damping, however, were successful in damping out weave and wobble oscillations.

One study has shown theoretically that, while a bike leaned in a turn, road undulations can excite the weave mode at high speed or the wobble mode at low speed if either of their frequencies match the vehicle speed and other parameters. Excitation of the wobble mode can be mitigated by an effective steering damper and excitation of the weave mode is worse for light riders than for heavy riders.